什么是整式方程概念是什么（八年级上数学期中知识点！）
100次浏览
发布时间：2024-11-10 10:48:59
知识结构：
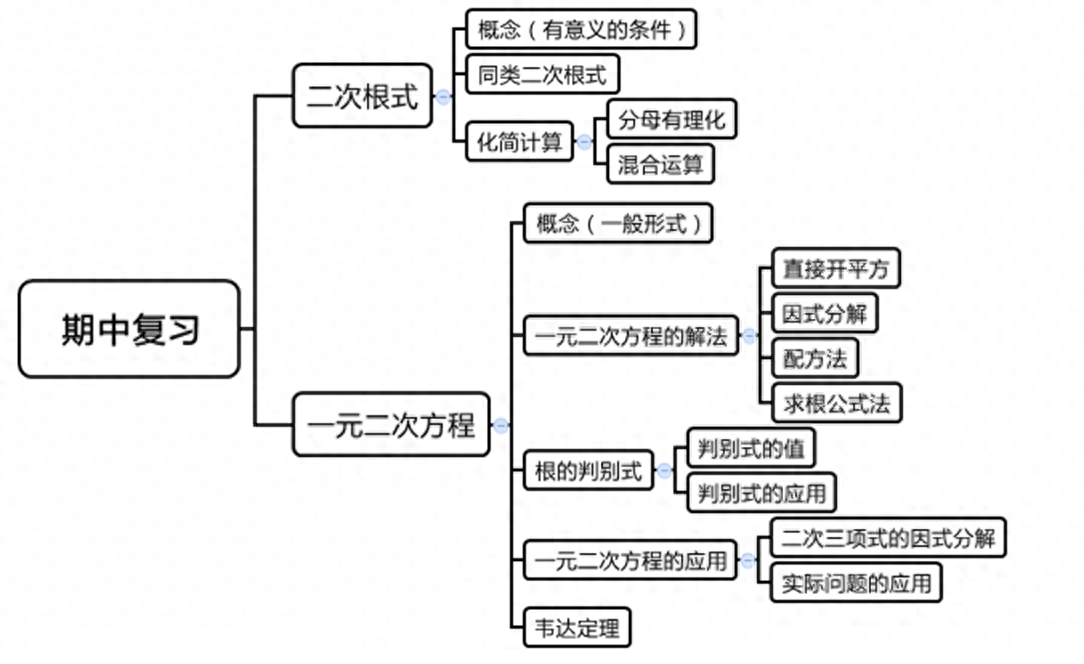
知识点汇总：
一、二次根式的概念
（1）代数式
（2）二次根式有意义的条件是被开方数是非负数．
二、二次根式的性质
三、二次根式的运算
1、最简二次根式：
（1）被开方数中各因式的指数都为1；
（2）被开方数不含分母．
被开方数同时符合上述两个条件的二次根式，叫做最简二次根式．
2、同类二次根式
几个二次根式化成最简二次根式后，如果被开方数相同，那么这几个二次根式叫做同类二次根式．
3、二次根式的运算
加减运算：把二次根式化简为最简二次根式，再合并同类项（加或者减）．
乘除运算：（1）两个二次根式相乘，被开方数相乘，根指数不变；（2）两个二次根式相除，被开方数相除，根指数不变．
4、分母有理化
（1）把分母中的根号化去就是分母有理化，即是指分母中不含二次根式的运算．
（2）分母有理化的方法：是把分子和分母都乘以同一个适当的代数式，使分母不含根号．
5、有理化因式
两个含有二次根式的非零代数式相乘，如果它们的积不含有二次根式，我们就说这两个含有二次根式的非零代数式互为有理化因式．
四、一元二次方程
1. 一元二次方程的概念
整式方程：方程的两边都是关于未知数的整式的方程叫做整式方程．
一元二次方程：只含有一个未知数，且未知数的最高次数是2的的整式方程称作一元二次方程．
2. 一元二次方程一般式
任何一个关于x的一元二次方程都可以化成ax² + bx + c = 0 (a≠0)的形式，这种形式简称为一元二次方程的一般式．其中ax² 叫做二次项，a是二次项系数；bx叫做一次项，b是一次项系数；c叫做常数项．
3. 一元二次方程的解
能够使一元二次方程左右两边的值相等的未知数的值叫做方程的解．只含有一个未知数的方程，它的解又叫做方程的根．
4. 特殊一元二次方程的解法
a) 直接开平方法
b) 因式分解法．
5. 一般一元二次方程的解法
a) 配方法：化成(a + m)² = n 的形式
b) 求根公式法：
6. 韦达定理
如果x1, x2是一元二次方程ax²+ bx + c = 0 (a≠0) 的两个根,由解方程中的公式法得
7. 判别式的值与根
1．一元二次方程根的判别式：我们把b² - 4ac叫做一元二次方程ax² + bx + c = 0 (a≠0)的根的判别式，通常用符号“△”表示，记作△=b²– 4ac．
2．一元二次方程ax² + bx + c = 0 (a≠0)，
当△=b²– 4ac＞0时，方程有两个不相等的实数根；
当△=b²– 4ac = 0时，方程有两个相等的实数根；
当△=b²– 4ac＜0时，方程没有实数根．
反之，也成立．
- 本文分类：常识
- 本文标签：无
- 浏览次数：100 次浏览
- 发布日期：2024-11-10 10:48:59
- 本文链接：https://m.ghbk.net/changshi/GRkg3zXJ4p.html
- 上一篇 > 秋波什么意思（暗送秋波）
- 下一篇 > 新手画眉毛的技巧图解（如何定眉头、眉尾、眉峰？）
