三点共线向量公式的应用（这几个例子，让你感受到向量的方便和强大之处！）
100次浏览
发布时间：2024-09-29 10:38:31
1、平面向量思维
本期内容和大家聊聊高中数学中的“平面向量”专题，人教版新教材改版之后，高一上册最后面学习的是“三角函数”，而“平面向量”专题放在了必修第二册的第一章，这样设置我觉得很合理，因为平面向量给我们提供了一个新的思维方式，让我们从另一个角度理解三角函数的定理和公式。
例如三角恒等变换公式可以利用向量内积证明，这种证明要比高一上册课本提供的“两点间距离公式”的证明方案更加简洁。
三角恒等变换两种证明方法对比
从上图很容易看出，借助向量工具的证明显然是要更加简洁一下的。
再比如解三角形中时离不开的“余弦定理”，余弦定理的证明虽然有很多方式，但是最简洁直接的依然是利用向量进行证明：
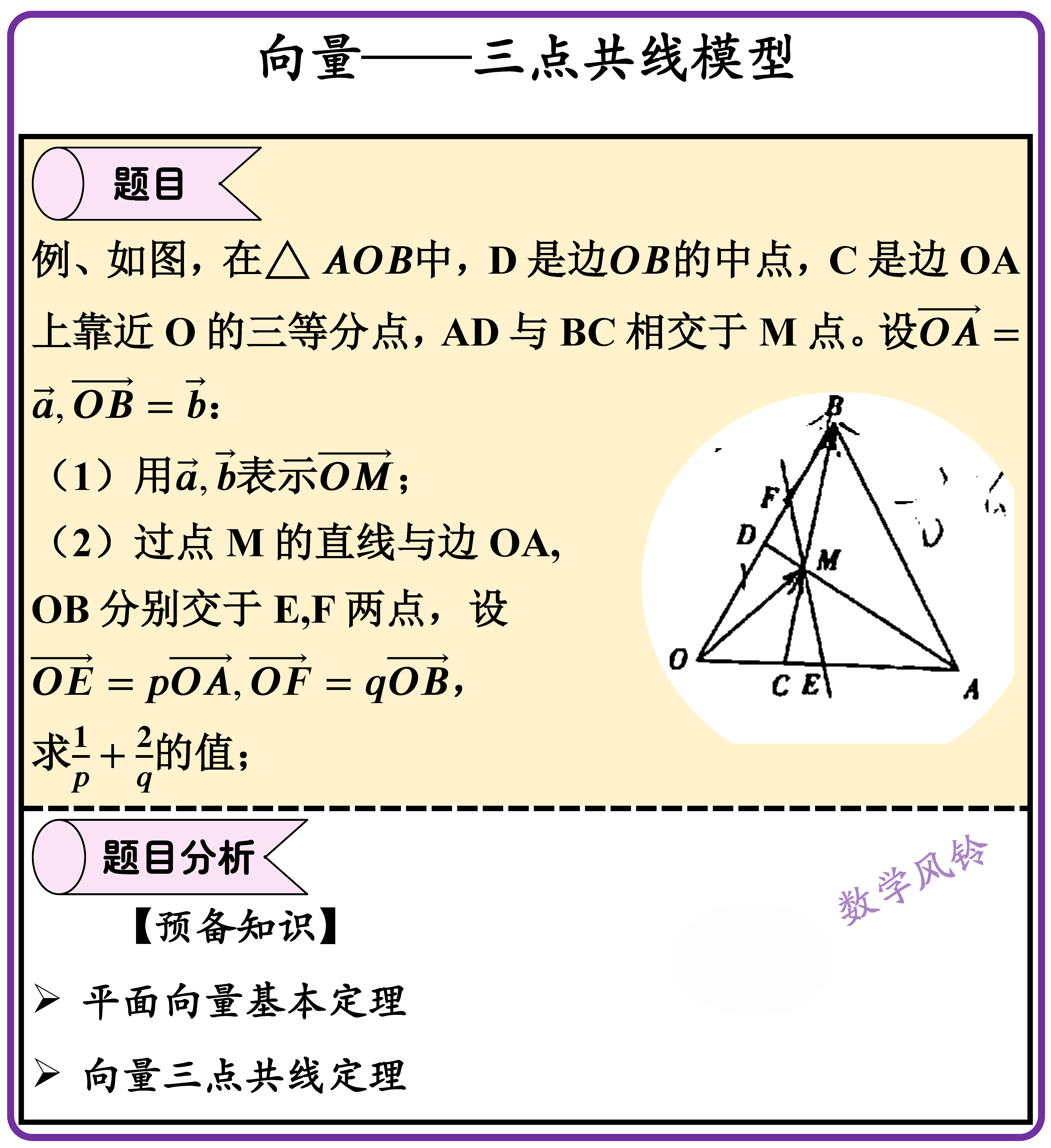
2、向量思维的养成——三点共线模型
高中数学之所以引入向量主题，在于向量本身的很多优点，以前我们处理平面几何中的问题时，基本上都是依据某些定理进行推导，一方面是证明过程繁琐；另一方面某些量的计算比较麻烦。但是同样一个问题，我们利用向量工具进行计算就显得非常简洁，除了开篇的两个例子外，我们再来讨论一个案例，感受一下向量这一工具的优势。
实际做题中，想要通过平角来证明三点共线是很难的，有的题目根本没有给出角度的信息，这个方案在具体做题中很难发挥作用，如果仅从传统平面几何的思路出发，三点共线的证明还是比较麻烦的。
但是当你学了向量之后，你会发现向量作为一个工具，在处理三点共线模型时真的是恰到好处，学过平面向量的人对三点共线模型肯定不会陌生，课本上有对应的例题，对应三点共线定理。
而向量方法先找到一组基底
下图例题解析
3、总结——学会用向量
本期分享的主要目的还是通过不同案例给大家展示向量这一数学工具的强大之处，我们展示了：三角恒等变换公式的证明、余弦定理以及三点共线模型的分析，每个案例都在说明用向量解决问题的确能简化分析。
对于大家来说，要学好一个知识点，你得先知道为啥学，肯定是这个内容有其独有的价值。我们得先找到向量的优势和价值，这样你才会被其价值折服，就会愿意主动去学习。
从我们三点共线模型的分析中其实也可以发现，向量工具在处理具体问题的时候一般都是建立在平面向量基本定理之上，先寻找基底，再用基底表示所需的向量，最后进行相关分析，其实这也是大家日后在做平面向量相关题目的主流思路，我们要去适应这种思路，学会把向量这一工具融会贯通！
- 本文分类：常识
- 本文标签：无
- 浏览次数：100 次浏览
- 发布日期：2024-09-29 10:38:31
- 本文链接：https://m.ghbk.net/changshi/yjLgD88gX9.html
